Nuclear Fusion Simulations on a Laptop
An overview of semi-analytic models for nuclear fusion schemes
Integrated three-dimensional simulations of fusion plasma experiments can take weeks on the world’s highest end supercomputers. But if you’re looking for an answer in much less time, seconds even, you can instead use a semi-analytic model, perfect for an old laptop.
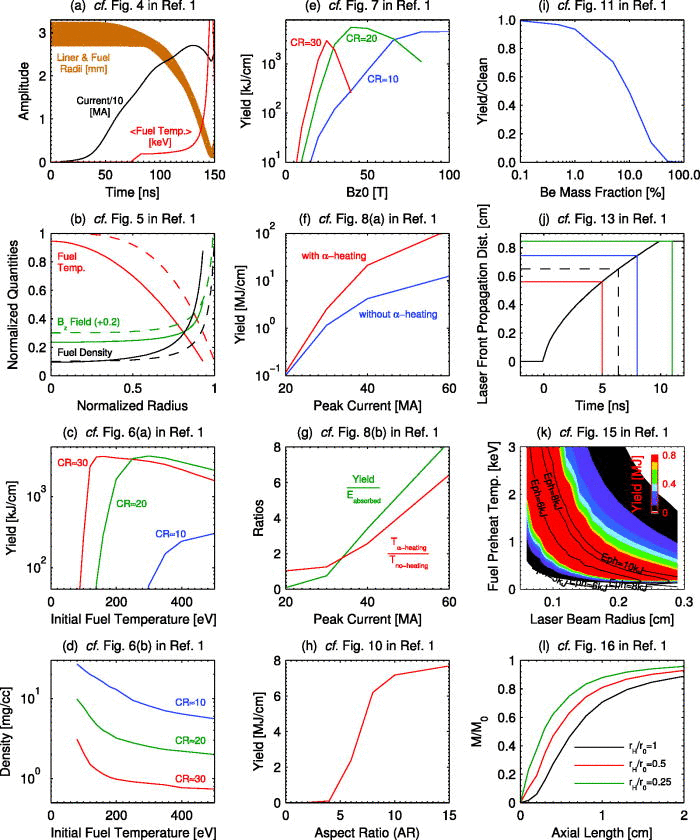
While more sophisticated codes are generally needed to fully model a fusion scheme, semi-analytic models often give reasonably accurate answers. They don’t account for all the physics or provide as much resolution, but they can help us better understand the physics going on, with a few simplifying assumptions, and by going to 1-dimension. This makes them more understandable and much faster so large parameter spaces can be explored.1 They can also provide quick and rough answers to many of questions relating to the scheme’s performance. For example, how does the fusion yield change based on the device’s dimensions, or the background magnetic field?
Lindemuth and Kirkpatrick pioneered the use of semi-analytic models for generalized magneto-inertial fusion back in the 80s.2 Even then, reasonable agreement was reached between their semi-analytic simulations and complete 2-dimensional MHD simulations. This is quite impressive considering how simplified the semi-analytic model is. More semi-analytic models, for different fusion schemes, have been developed in recent years, three of which I discuss below.
All of them are essentially just a few equations that represent the key physical processes of the fusion scheme. These are usually a set of ordinary differential equations that are integrated in time, which puts the “semi” in front of “analytic”. Taken together they tell you a lot about how the fusion scheme works, and, in some cases, how you can directly modify certain variables to achieve your desired outcome. You can’t get that same direct insight just by reading through the more sophisticated fusion/plasma simulation codes because they use more fundamental physics equations (like the fluid and radiation transfer equations).
MagLIF
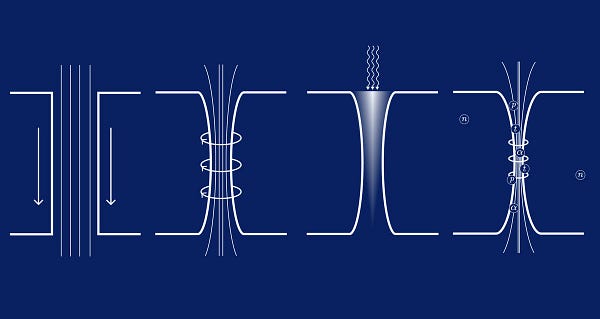
To make semi-analytic models more concrete, let’s take a look at SAMM,3 a semi analytic model for magnetized liner inertial fusion (MagLIF), and a few of its equations. Note that many semi analytic models developed recently take inspiration from SAMM, so if you understand SAMM, it won’t be as a big a leap to understand the others.
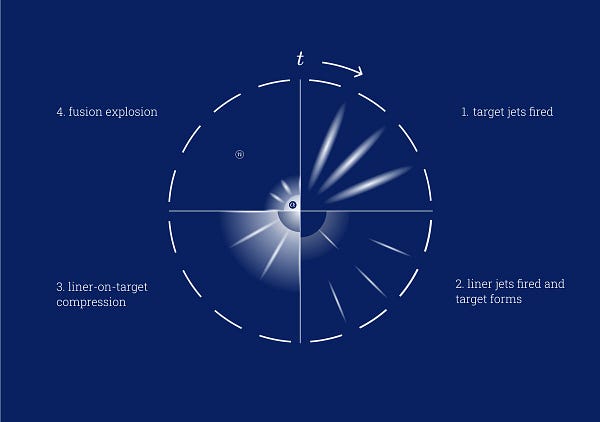
If you don’t know much about MagLIF, you can quickly get up to speed with the visualization below.

Now let’s go over just three of SAMM’s equations to a get sense of how these semi-analytic models work.
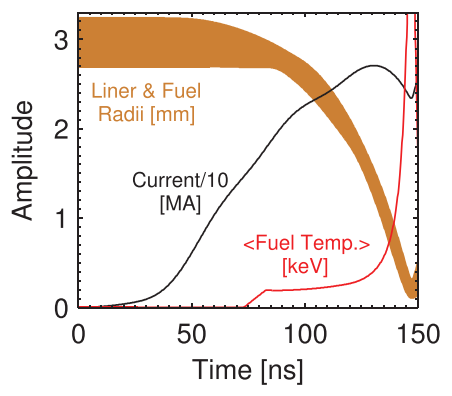
The liner is split into a number of interfaces and Eq. (171d) calculates their radial accelerations. By integrating this in time we can we get the trajectory of the liner. Similar equations are written down for other radial positions we want to track, like the radius of the the inner side of the liner.
The energy (mostly thermal energy) of the gas region changes according to these 6 terms from left to right: pdV compression work, laser preheat power, alpha heating power, radiation losses, thermal conduction losses, and energy end losses. This is actually a fairly general list of power terms that can be applied to most fusion schemes, particularly the alpha heating, radiation losses, and thermal conduction losses.
We can also calculate the number of fusion reactions occurring at each step. So by the end of a simulation we can then determine the total yield.
There are about a dozen more unique equations in the ODE system. A lot more equations are needed to calculate the variables needed for the ODE system equation, but they are no more difficult to understand the ones written above. In any case, it’s pretty amazing that one can model such an intricate and nonlinear implosion process with this relatively simple set of equations.
Staged Z-Pinch
A semi analytic model has also been made for the gas-puff staged z-pinch concept.4

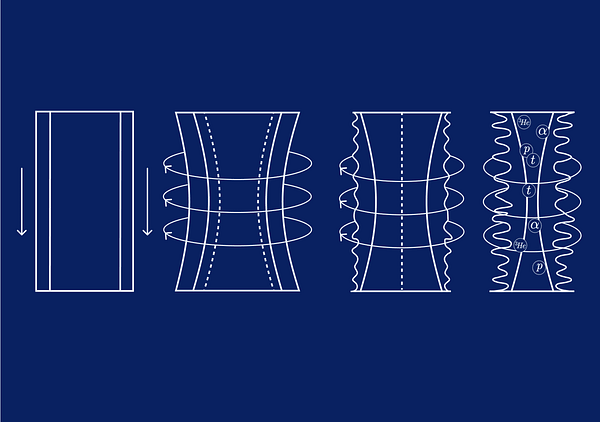
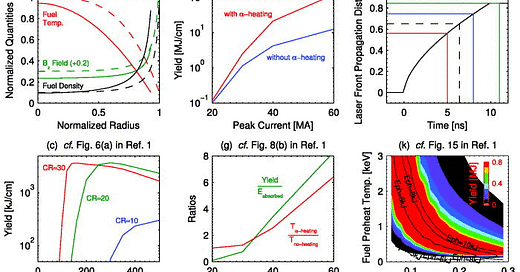
It builds on SAMM with a few modifications that incorporate the physics important to staged z-pinches, such as azimuthal magnetic field transport (as opposed to just axial magnetic field transport), shock heating of the fuel, and different energy equations for the ions and electrons (because their equilibration time may exceed the implosion time). Below are two plots visualizing some simulation results from this semi-analytic model.
Plasma Jet Driven Magneto Inertial Fusion (PJMIF)
The last semi-analytic model I’ll discuss here is for PJMIF.5

Even though PJMIF has a spherical geometry, rather than a cylindrical geometry like the previous 2 schemes, and a plasma liner, rather than a solid liner, this semi-analytic model is not all that different from SAMM. For example, the liner is still split up into a set of interfaces and evolved according to a pressure balance. Of course there are some differences, and these need to be addressed to reasonably model the implosion, like the liner formation.
Semi analytic models for fusion are useful for the large parameters scans that full 3d-codes are too slow for, but they’re also great learning tools. So if you’re interested in learning more I recommend reading the papers I referenced earlier (in the footnotes). Even better, you can try to reproduce one of these semi-analytic models. If you want to learn more about the physics of fusion, they’re a great way of progressing past the pop-sci of most fusion media coverage, and gaining a real intuition for the physics behind a fusion scheme.
As an example, you could vary the initial target/plasma density and magnetic field and run hundreds or thousands of simulations and see how the fusion yield is affected.
I.R. Lindemuth and R.C. Kirkpatrick 1983 Nucl. Fusion 23 263
Ryan D. McBride and Stephen A. Slutz, "A semi-analytic model of magnetized liner inertial fusion", Physics of Plasmas 22, 052708 (2015) https://doi.org/10.1063/1.4918953
Narkis, J., Rahman, H. U., Valenzuela, J. C., Conti, F., McBride, R. D., Venosa, D., and Beg, F. N. Wed . "A semi-analytic model of gas-puff liner-on-target magneto-inertial fusion". United States. https://doi.org/10.1063/1.5086056. https://www.osti.gov/servlets/purl/1574129
Samuel J. Langendorf and Scott C. Hsu, "Semi-analytic model of plasma-jet-driven magneto-inertial fusion", Physics of Plasmas 24, 032704 (2017) https://doi.org/10.1063/1.4977913



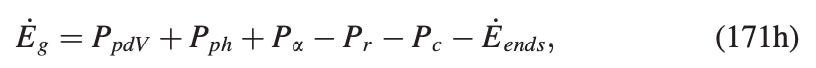




Finally! A Substack about Fusion 😀 this is cool.